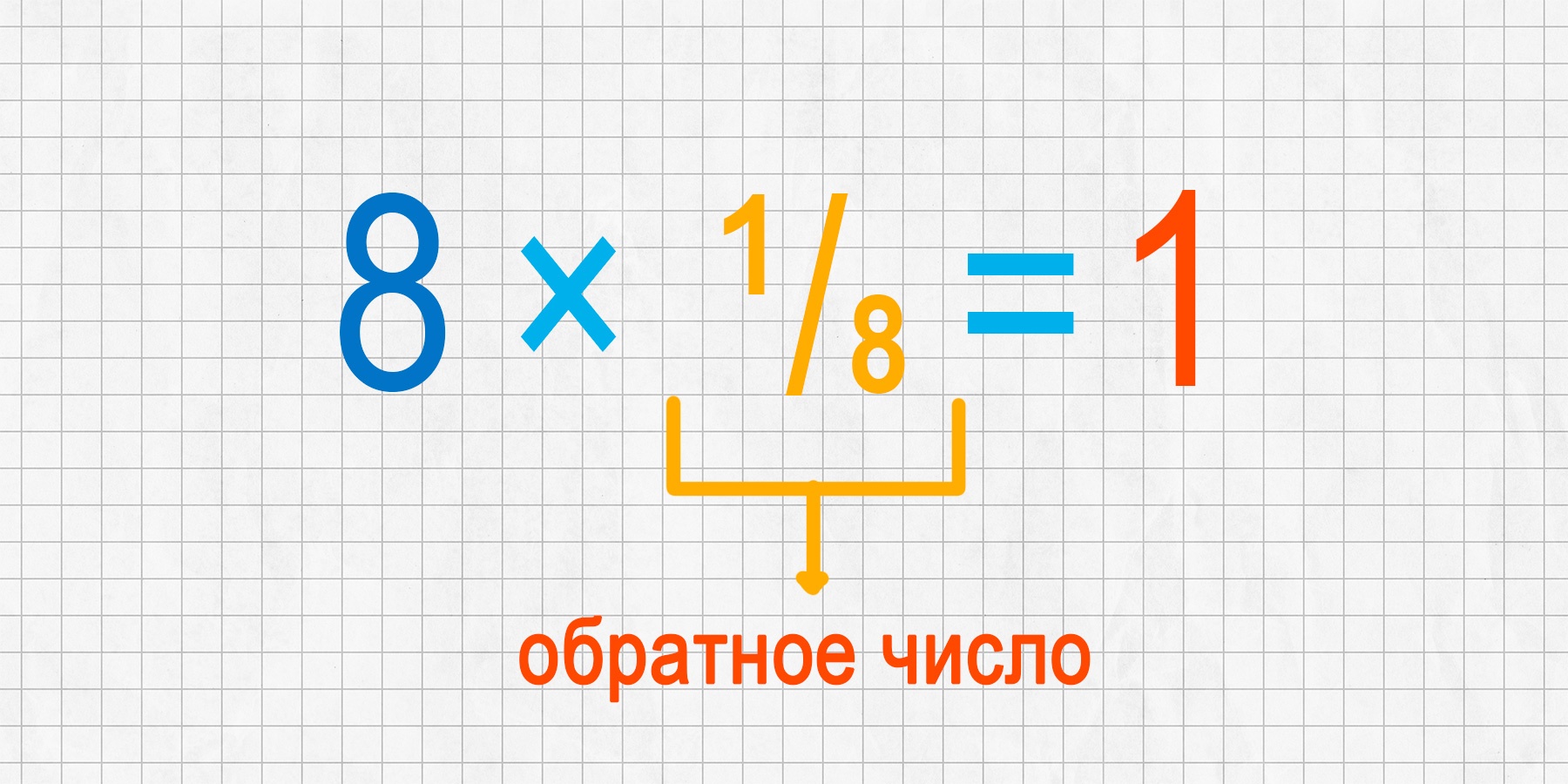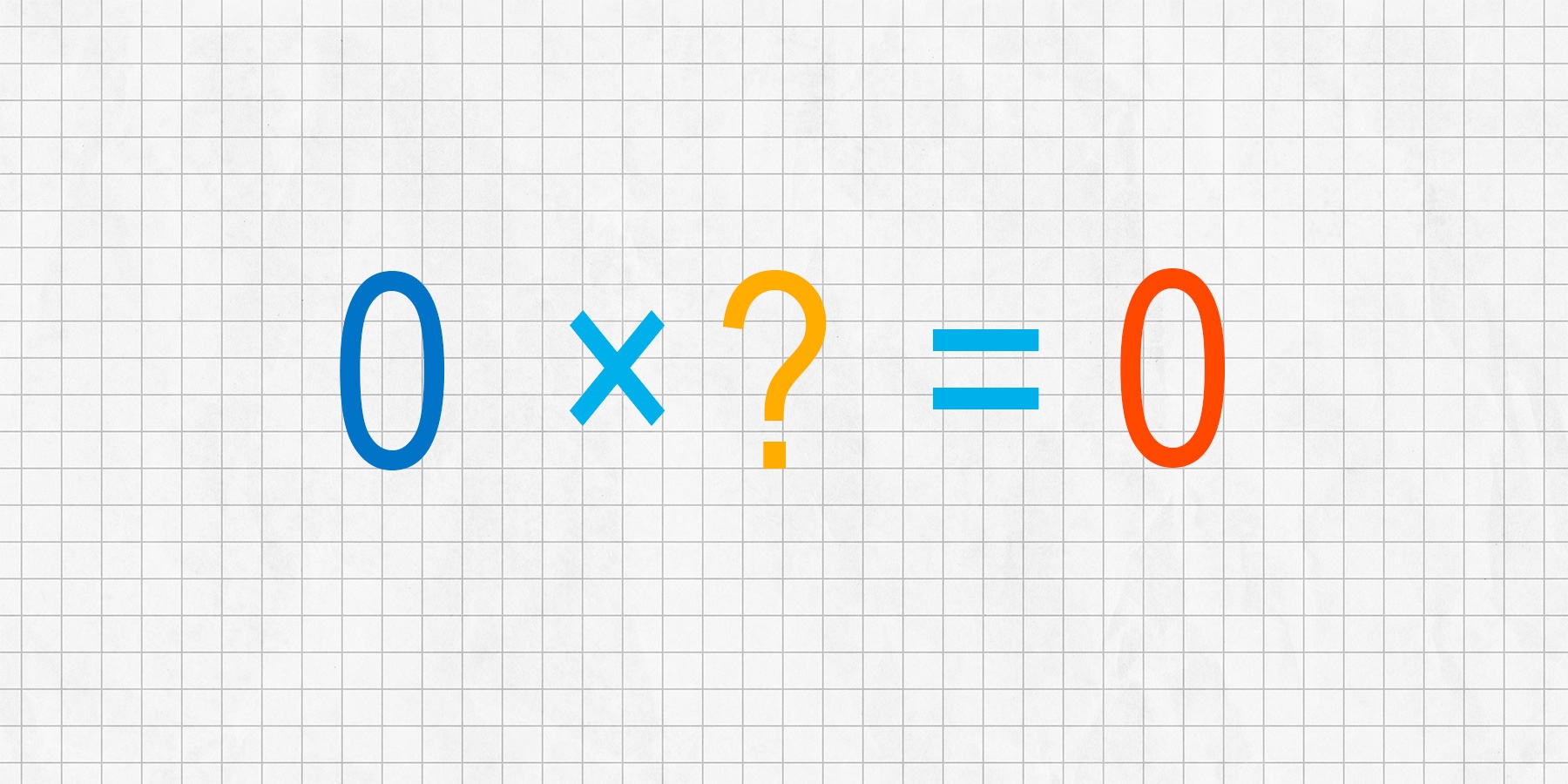Что такое деление?
Прежде чем пытаться делить на ноль, нужно понять, что вообще такое деление и как оно работает. Возьмем для примера число восемь и поделим его на несколько чисел: 8:8 = 1, 8:4 = 2, 8:2 = 4, 8:1 = 8. Можно заметить, что чем меньше число, на которое мы делим, тем больше получается результат от деления. Логично предположить, что, если делитель уменьшить еще сильнее, до нуля, частное вырастет до бесконечности. Но так ли это на самом деле?
Математики знают лишь то, что, если делитель стремится к нулю, частное стремится к бесконечности. Но это вовсе не значит, что результат деления на ноль равен бесконечности.
Давайте введем еще одно понятие — обратные числа. Что это?
Посмотрим на те же примеры с другой стороны. При делении восьми на два получается четыре. Тот же самый результат можно получить, умножив восемь на одну вторую: 8:2 = 4 → 8 × ½ = 4. А чтобы из восьми получить единицу, можно либо разделить восемь на восемь, либо умножить восемь на одну восьмую. Получается, что деление можно заменить умножением — для этого достаточно заменить второе число в примере на «перевернутую» версию себя или на обратное число: 8:8 = 1 → 8 × ⅛ = 1.
Почему у нуля нет обратного числа?
Взаимно обратные числа обладают еще одним важным свойством: их произведение всегда равно одному: 8 × ⅛ = 1; 5 × ⅕ = 1; 2 × ½ = 1. Значит, вместо того, чтобы пытаться разделить какое-то число на ноль, достаточно умножить его же на обратное нулю число. Какое число обратно нулю? Такое, которое при умножении на ноль давало бы единицу: 0 × ? = 1. Но не существует числа, которое при умножении на ноль дало бы что-то кроме нуля!
Можно ли ввести специальное число, обратное нулю?
В математике так нередко делают — например, нельзя извлечь квадратный корень из -1. Но математики ввели специальное число i = √-1, которое открыло много возможностей работы со сложными числами. Мы могли бы договориться, что знак бесконечность ∞ означает нужное нам обратное нулю число: ∞ = 1/0. Можно ли таким числом пользоваться и совершать операции?
0 × ∞ = 1. Пока все в порядке. Тогда 1+1 = 2 можно представить как (0 × ∞) + (0 × ∞) = 2. Это выражение можно сократить до (0 + 0) × ∞ = 2. Но получившееся выражение 0 × ∞ = 2 противоречит нашим изначальным условиям!
Число, обратное нулю, не работает в привычной нам математике и нарушает все ее правила.
Позволяет ли математика делить сам ноль на ноль?
Если попытаться разделить ноль на ноль, ситуация меняется: в таком случае нужно подобрать число, которое при умножении на ноль дало бы ноль: 0 × ? = 0. Получаем проблему, противоположную предыдущей, ведь на этот раз под интересующее нас условие подходит любое число. А так как однозначный ответ выбрать невозможно, говорят, что результат деления нуля на ноль не определен.
Получается, что разделить ноль на ноль нам мешает отсутствие однозначного результата. Любое другое число разделить на ноль не получается из-за самого определения деления как действия, обратного умножению: нет таких чисел, которые при умножении на ноль давали бы не ноль. А значит, и деление на ноль в обычной математике просто не имеет смысла.